전제: 하이퍼파라미터 튜닝이 중요한 이유?
- 딥러닝 모델의 성능은 학습률, 은닉 뉴런 수, 배치 크기 등 하이퍼파라미터에 크게 좌우됨
- 하지만 가능한 조합은 너무 많고,
→ 모든 조합을 다 실험하기는 불가능
→ 그래서 현실적인 탐색 전략이 필요해요
Coarse-to-fine Sampling Scheme
의미:
처음에는 넓고 거칠게 탐색하고,
가능성 있는 영역을 찾으면 그 근처를 좁고 촘촘하게 탐색하자!
단계적 접근:
- Stage 1: Coarse Sampling
- 예: learning rate ∈{0.0001,0.01,1}\in \{0.0001, 0.01, 1\}, batch size ∈{8,64,512}\in \{8, 64, 512\}
- 빠르게 전체 지형을 살펴보는 느낌
- 약간 부정확하더라도 성능이 급격히 떨어지는 조합은 빠르게 제외 가능
- Stage 2: Fine Sampling
- 예: learning rate ∈{0.005,0.01,0.02}\in \{0.005, 0.01, 0.02\}
- 가능성 있는 조합 근처를 더 세밀하게 탐색
장점:
- 탐색 비용을 줄이면서도 좋은 조합에 빠르게 수렴 가능
- 시간과 자원을 절약하면서 성능 최적화 가능
Grid Search vs Random Search
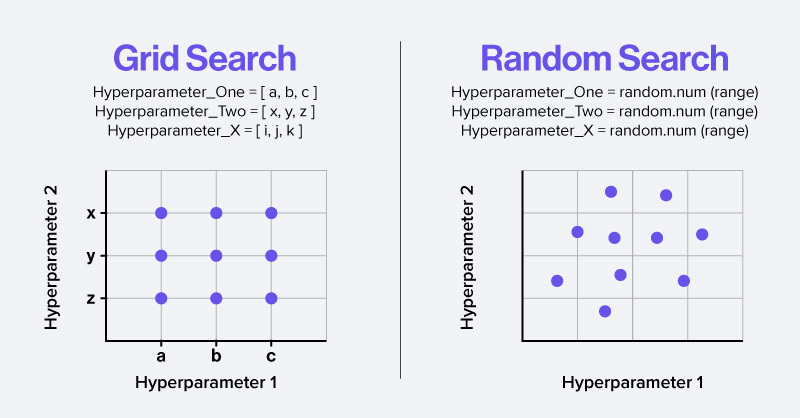
1. Grid Search
모든 하이퍼파라미터 조합을 격자 형태로 전부 탐색
예시
| Learning Rate | Batch Size |
| 0.001 | 32 |
| 0.001 | 64 |
| 0.01 | 32 |
| 0.01 | 64 |
문제점:
- 고차원에서는 비용 폭발 (curse of dimensionality)
- 어떤 하이퍼파라미터가 성능에 중요한지 몰라도,
모든 조합을 균일하게 탐색하므로 비효율적
2. Random Search
탐색 범위 내에서 랜덤하게 조합을 선택하여 탐색
예시:
- 학습률: Uniform[0.0001, 0.1]
- 은닉 유닛 수: Uniform[32, 512]
→ 각 trial마다 이 범위에서 무작위로 뽑아서 학습
장점 (왜 더 효율적인가?)
- 성능에 영향을 미치는 하이퍼파라미터에 더 집중
- 비영향 변수에 낭비하지 않음
- 예를 들어:
- 학습률이 성능에 민감하지만 배치 크기는 별로 영향 없다면?
- Grid search는 배치 크기에도 불필요하게 시간 낭비
- Random search는 더 다양한 학습률 값을 테스트하게 됨
🔬 실험적으로도,
Random Search는 Grid보다 적은 실험으로 더 나은 성능을 찾는 경우가 많음
(참고: Bergstra & Bengio, 2012)
Random Search를 쓸 때 "무작위로 어떻게 뽑을 것인가?"
어떤 확률 분포에서 샘플링하는 것이 적절한가?
1. Binary / Discrete 하이퍼파라미터
ex: optimizer 종류, activation function, batch size, layer 수 등
사용 분포:
- Bernoulli 분포: 두 값 중 하나 → (예: True/False, on/off)
- Multinoulli (Multinomial의 특수한 경우): 여러 개 중 하나 선택 → (예: [SGD, Adam, RMSProp] 중 택 1)
import random
optimizer = random.choice(['SGD', 'Adam', 'RMSprop'])
use_dropout = random.choice([True, False])
2. Positive Real-Valued 하이퍼파라미터
ex: learning rate, weight decay, dropout rate, regularization strength 등
문제:
- 이런 값들을 선형적으로 (uniform하게) 뽑으면,
작은 값들이 무시되고 대부분 큰 값만 실험하게 됨
예:
0.0001 ~ 1 사이에서 Uniform(0.0001, 1)을 뽑으면,
대부분 0.8~1 같은 값만 나옴 → 0.001 같은 작은 값은 거의 안 나옴

해결책:
log-scale에서 균등분포로 샘플링
import numpy as np
epsilon = 10 ** np.random.uniform(-4, 0) # → 0.0001 ~ 1 구간에서 log-uniform 샘플링
- 이렇게 하면 log(0.0001), log(0.001), log(0.01), log(0.1), log(1) 사이에서 동등하게 선택 가능
- 즉, 작은 값들도 공정하게 탐색할 기회를 가짐
예시 비교
| 방법 | 결과 |
| Uniform(0.0001, 1) | 대부분 큰 값(0.7, 0.9) 위주로 나옴 |
| Log-Uniform(-4, 0) | 0.0001, 0.001, 0.01, 0.1 등 다양한 scale 고루 탐색 |
결론 요약
| 하이퍼파라미터 타입 | 추천 샘플링 분포 |
| Binary | Bernoulli |
| Discrete (다중 클래스) | Multinoulli |
| Positive real-valued | Log-uniform (log-scale 균등) |
'AI 및 Data Analysis > Deep Learning' 카테고리의 다른 글
| [Asymmetric Attributes] Concepts (0) | 2025.04.18 |
|---|---|
| [Law of Large Numbers] Key Concepts (0) | 2025.04.17 |
| [Weight Initialization] Concept (0) | 2025.04.16 |
| [StratifiedKFold] Key Concepts and Descriptions (0) | 2025.03.27 |
| [Optuna] Key Concepts and Descriptions (0) | 2025.03.27 |


