[Cost Function] Linear Regression & Logistic Regression

 

선형 회귀(Linear Regression)

손실 함수: $J(\mathbf{w}) = \frac{1}{N}\sum_{i=1}^N (\mathbf{w}^\top \widetilde{\mathbf{x}}_i - y_i)^2$ (MSE)

 

해석적 해(정규방정식)가 존재: $\mathbf{w}^* = (\widetilde{X}^\top \widetilde{X})^{-1}\widetilde{X}^\top \mathbf{y}$

 

하지만
$N$이 너무 크거나,
$d$가 너무 커서 $(X^\top X)^{-1}$ 계산이 부담스럽거나,
온라인 학습/메모리 제약상 정규방정식을 못 쓸 때,
$~\widetilde{X}^\top \widetilde{X}$가 특이(singular)해서 역행렬이 안 만들어질 때
→ Gradient Descent(SGD, Mini-batch, Batch GD 등)를 사용하여 선형 회귀를 학습할 수 있다.

---

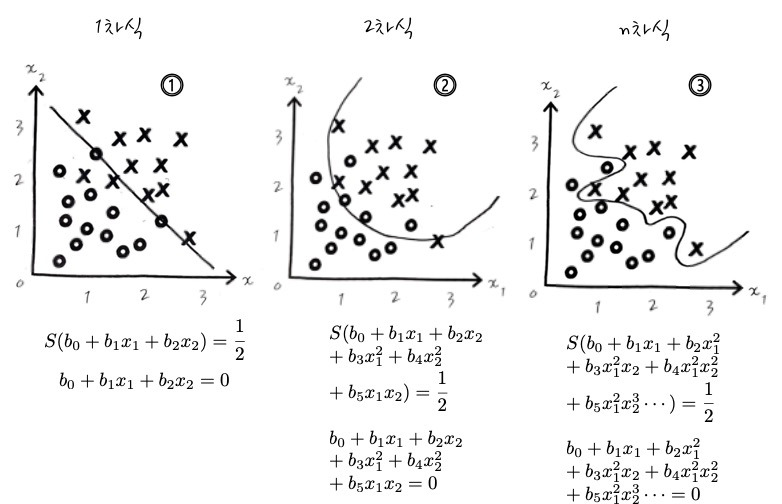
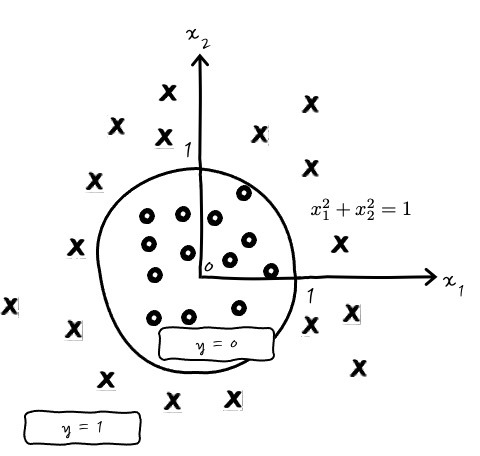
로지스틱 회귀(Logistic Regression) ; 이진 분류를 위한 decision boundary (hyperplane) 선형 함수이다.

요기에서 두 x에 대한 평면에 있는  b0+b1x1+b2x2=0b0+b1x1+b2x2=0  직선이 확률세로축(z축)으로 쭈욱~ 벽처럼 서게 되면, 이 평면이 Decision Boudary이라고 부르는 결정 경계가 되겠습니다.

손실 함수: Negative Log Likelihood (Binary Cross‐Entropy)

$ L(\mathbf{w}) = -\sum_{i=1}^N \Bigl[y_i \ln(\sigma(\mathbf{w}^\top \widetilde{\mathbf{x}}_i)) + (1-y_i)\ln(1-\sigma(\mathbf{w}^\top \widetilde{\mathbf{x}}_i))\Bigr]$

해석적 해(Closed-form solution)가 존재하지 않기 때문에,
→ 무조건 경사 하강법(혹은 Newton, Quasi-Newton 등 반복 최적화 기법)을 이용해 $\mathbf{w}$를 찾아야 한다.

---

결론

“선형 회귀에서는 Gradient Descent를 안 쓰는가?” → 아니다. 쓸 수 있다. 다만, 선형 회귀는 해석적 해가 있기 때문에 보통 그걸 쓰고, 특별히 데이터가 매우 크거나 차원이 높아서 그게 불가능할 때만 경사 하강법을 쓴다.

“Logistic Regression에서만 Gradient Descent를 쓰는가?” → 경사 하강법은 Logistic Regression에서 반드시 필요하지만, Linear Regression에서도 충분히 쓸 수 있다. 단, Linear Regression은 해석적 해가 있으므로 많은 경우에 정규방정식을 이용해 한 번에 푸는 편이 좀 더 간단하다.

---

사진 출처

https://recipesds.tistory.com/entry/Decision-Boundary-Logistic-Regression%EA%B3%BC-Classification%EC%9D%98-%EC%B0%A8%EC%9D%B4

Decision Boundary- Logistic Regression과 Classification의 차이

* Logistic 더 자세한 설명 참고