RECOVERING TIME-VARYING NETWORKS FROM SINGLE-CELLDATA

[PAPER] RECOVERING TIME-VARYING NETWORKS FROM SINGLE-CELLDATA

https://arxiv.org/abs/2410.01853

Recovering Time-Varying Networks From Single-Cell Data

---

 

 

2. MEHODS

2.1 PROBLEM SETUP

• X는 $cell*gene$ Matrix 형태.
  • gene은 25,000~35,000
  • cell은 수천개~수백만개
• Dynamic Graph에서 cell에 time이 있다고 가정해보자.
  • 그럼 $X_t $ 는 $cell_t * gene$ 형태
    • $cell_t$는 $t$마다 달라질 수 있음
• Directed graph $\widetilde{G} := {G1, ... , G_T}$를 복원하는 것이 목표이다.
  • graph node는 gene의 집합. $N=[g]$ ; static
  • graph edge는 $\varepsilon_t = {(u,v,x)}$; dynamic
    • v : target
    • u : target v의 발현을 조절하는 gene
    • w : 이 관계의 강도
    • source node를 전사 인자 유전자(TF)라고 합니다.
• $ G_t $를 $A_t$로 특성화하자. 
  • $ \widetilde{X} = f ( \widetilde{X} ^ {TF}, \widetilde{A} )  $
    • $ \widetilde{X} ^ {TF} $ 는 모든 $TFs$의 발현을 나타냄
    • f는 복잡해서 알려져있지 않음
    • f를 autoencoders로 학습하기도 함
    • 하지만 모든 gene expression을 reconstruction 하기엔 어렵다.

$ \widetilde{X} $ 는 원래 데이터로 우리가 가진 input입니다.

그러나 여기서 이 수식은:
 "$\widetilde{X}_{\text{TF}}$ 와 모델이 학습한 $\widetilde{A}$으로 전체 발현 $\widetilde{X}$를 복원할 수 있는지 보는 reconstructive insight"입니다.

즉, 이건 "생물학적으로 f라는 함수가 존재한다고 가정"하는 것이고, 실제로는 Marlene은 이걸 직접 복원하려 하기보다는, 이를 활용해서 cell type 분류로 우회 학습합니다.

 

• GRNs는 cell function에 의존한다. => cell type 예측 문제로 단순화해보자!
  • 이는 GRNs 복구도 가능하게 할 것이다.
  • 분류 문제 $y = f ( \widetilde{x}  ^{TF} , \widetilde{A} )$
    • $ \widetilde{x} ^ {TF}$ : 동일한 유형의 세포로 구성된 시간적 배치가 주어졌을 때
    • $ \widetilde{x} ^ {TF} ∈  ℝ ^ {T×배치 크기×n}$
    • y는 정답 cell type

2.2 ARCHITECTURE OF MARLENE

Marlene은 세 가지 주요 단계로 구성됩니다. 

처음 두 단계는 (1)에서 h의 선택을 다루고, 

마지막 단계는 f의 선택을 다룹니다.

 

< first step : 유전자 특징화 단계 >

• input : $X$ (cell*gene)
• method : PMA (Pooling by Multihead Attention) ; “세포” 위에서 작동 ; PMA는 attention을 "세포들을 요약하는 통계"로 활용
• output : $G = H^T$ (gene*k feature)
  • k : 모델이 학습하고자 하는 '출력 통계 벡터의 수', 즉 "pooling summary vector의 개수"를 의미. PMA가 학습한 집합의 요약 통계(vector summary)를 나타냄

* 하나의 batch에는 -> 하나의 cell type만 데이터로 주어져야한다!

 

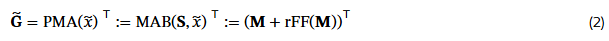
단계	연산 이름	적용대상	목적	Query/Key/Value	구조 출력	비유
1단계	PMA (Pooling by Multihead Attention)	**세포(Cell)**들	각 유전자에 대한 통계 요약 벡터 생성	Query: 학습 가능한 Seed vector $S$ Key/Value: $X \in \mathbb{R}^{c \times g}$	$H  \in \mathbb{R}^{k \times g} $ → 전치 → $G \in \mathbb{R}^{g \times k}$	“여러 사람들(세포)의 의견을 듣고 요약하는 작업”
2단계	Self-Attention (GRN 학습용)	**유전자(Gene)**들	유전자 간 조절 관계 (GRN) 추론	Query/Key:  $G_t W_t^Q, G_t W_t^K $ from gene feature $G_t$	Adjacency matrix  $A_t \in \mathbb{R}^{g \times g}$ (혹은 $g \times p$)	“요약된 전문가들(유전자)끼리 서로 대화하며 관계도를 그리는 작업”

한줄 요약
PMA: 세포들을 정리해서 유전자별 표현을 만드는 attention → “요약 pooling”
GRN Self-Attention: 유전자 표현들 간의 관계를 모델링하는 attention → “유전자 네트워크 학습”

비유로 쉽게 이해하면?
1단계 PMA는 “여러 사람들(세포)의 의견을 듣고 요약하는 작업”
2단계 Self-Attention은 “요약된 전문가들(유전자)끼리 서로 대화하며 관계도를 그리는 작업”

 

< second step : self-attention >

• input : $G_t$
• method : self-attention 시행.; “유전자” 위에서 작동 ; GRN을 위한 “유전자들 사이의 상호작용( 유전자 간의 관계, 조절 방향(→) )을 모델링”하는 attention
• output : $A_t$ ; gene regulatory network, 즉 directed weighted graph
• 생물학적 타당성과 계산 효율성을 위해 열(즉, 조절자 역할을 하는 유전자)을 TF(transcription factors)로 제한하여 $A_t \in \mathbb{R}^{g \times p}$ 로 만듭니다.
  • 여기서 $p$는 TRRUST 데이터베이스에 있는 알려진 TF의 수입니다.

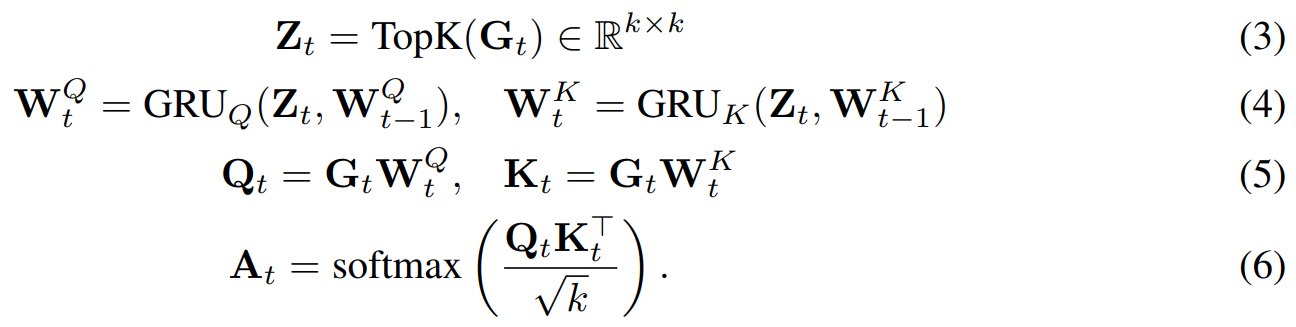
*  GRU를 통해 self-attention의 Query/Key weight $(W_t^Q,W_t^K)$ 가 시간 t에 따라 변하도록 구성
즉, 이전 시간 $t−1$의 weight를 기반으로 → 현재 시간 t의 weight를 GRU를 통해 "진화(evolve)"시킴
=> W가 스스로 시간에 따라 업데이트 되도록 구성된 것!

* Since most time series we deal with contain very few time points, a GRU should suffice and not suffer from vanishing gradient problems.
우리가 다루는 대부분의 시계열은 시간 지점이 매우 적기 때문에 GRU로 충분하며 기울기 소멸 문제가 발생하지 않습니다.
→ Marlene이 다루는 scRNA-seq 시계열 데이터는 보통 시간 지점 수가 적음 (예: 4~7)
→ 따라서 복잡한 LSTM보다는 GRU가 적합

* 상위 중요 유전자 𝑘개만 뽑아 정사각 행렬 $Z_t∈R^{k×k}$ 생성 → GRU 입력으로 사용

 

< Last Step: Gene Expression Reconstruction & Cell Type Prediction >

• input : $ \widetilde{x} ^ {TF} \widetilde{A} ^ {T}  $ → TF 유전자들의 발현값과 복원된 시간별 GRN $\widetilde{A}$를 조합한 표현
• method : 여러 개의 fully connected (FC) layer + 비선형 활성화 함수 $\sigma$
• output : $ \widetilde{y} ∈R^C $ → 총 cell type 수만큼의 logit vector
  → CrossEntropyLoss를 통해 학습

*  $A_t∈R^{g×p}$ → $A_t^⊤∈R^{p×g}$

* $x ̃^{TF}  A ̃^⊤ ∈ R^{cell× g} $ 즉, TF의 발현과 gene 연결 정보(GRN)를 곱해서 전체 유전자 발현값(cell type 예측)을 얻는 형태